双指针的用途
双指针法一般用于什么问题?首先,我们需要考虑是单向还是双向的。
单向双指针:
- 链表:找倒数第几个位置,或者找中间的位置
- 数组:覆盖,交换,重新构造秩序,单向覆盖
双向双指针:
- 倒序,交换,快速排序(递归)
- 有序数组的两个数之和,正负数有序的平方,也就是满足前后的双数查找
单向双指针
- 链表:找倒数第几个位置,或者找中间的位置
- 数组:覆盖,交换,重新构造秩序,单向覆盖 话不多说上例题
1. 链表的中间节点
给定一个头结点为 head 的非空单链表,返回链表的中间结点。 如果有两个中间结点,则返回第二个中间结点。
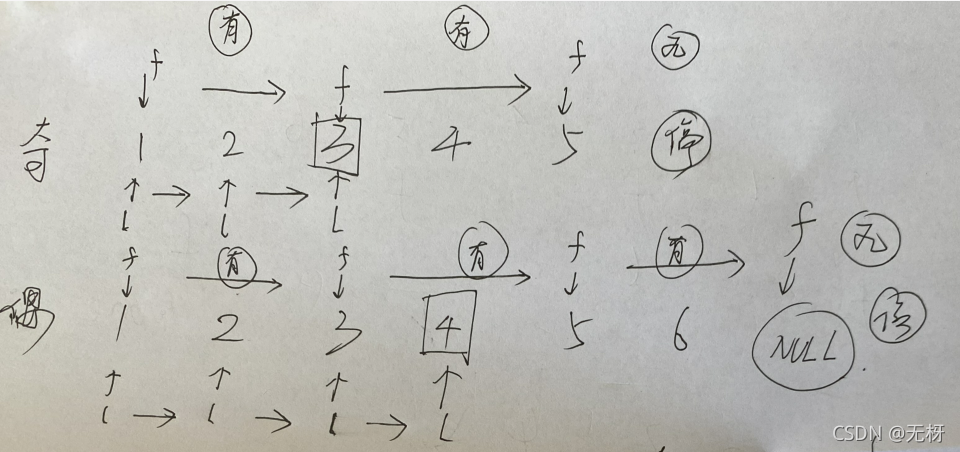
解法1,首先朴素解法肯定是先遍历一遍单链表,求出单链表的长度,然后再遍历一半链表即可。 时间复杂度:首先要遍历一遍单链表,然后遍历一遍,所以时间复杂度O(3n/2) 空间复杂度:并未借助辅助空间O(1) 解法2,利用双指针,一个快指针一个慢指针,快指针一次走两步,慢指针走一步,如果快指针到头了,那么慢指针指到中间节点 注意考虑边界条件。
class Solution(object):
def middleNode(self, head):
"""
:type head: ListNode
:rtype: ListNode
"""
if not head:
return
l=head
f=head
while f and f.next:
l=l.next
f=f.next.next
return l
这里要判断f和f的next是否为空,如果有一个为空就要停止,不然fast指针会越界。
## 2. 删除链表的倒数第N个节点 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 进阶:你能尝试使用一趟扫描实现吗?
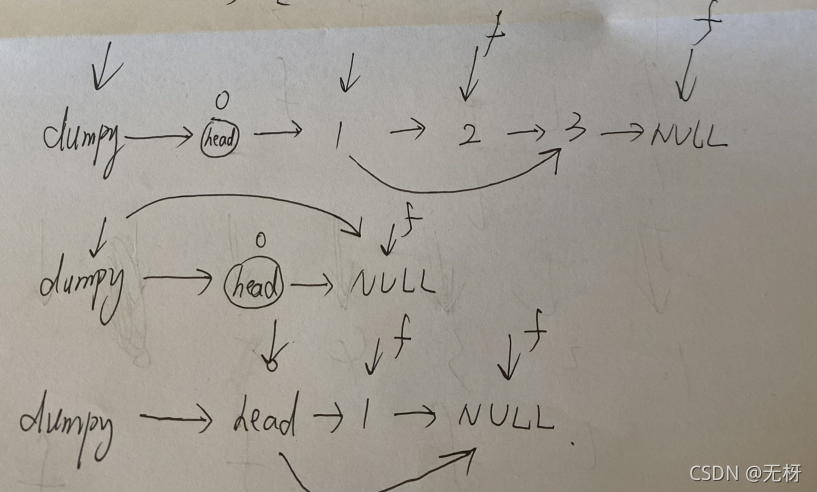
解法1,朴素做法::先遍历一遍单链表,求出单链表的长度,然后再遍历到长度减去n的链表长度-1然后实现单链表的删除即可。 解法2,利用双指针,先用一个快指针走n步,然后一个慢指针和快指针同步行走。当快指针走到末尾的时候,慢指针到达的位置正好是可以是用单链表删除的位置。 在这里我们要考虑边界情况: 当输入链表0个元素的时候,返回none 当输入链表1个元素的时候,也要执行删除操作,所以慢指针作为我们的结果指针应该要在头指针之前。返回也是none
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
dummy = ListNode(0, head)
first = head
second = dummy
for i in range(n):
first = first.next
while first:
first = first.next
second = second.next
second.next = second.next.next
return dummy.next
这里dummy是头指针前面一个,然后慢指针second首先要在这个位置,然后等first移动n步,之后同步移动,first为null的时候,second指向要删除的元素的前一个,然后执行删除。
3. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
解法1,置0,双指针,碰到0则将其位置赋非零数值,然后最后将多出来的部分全部置零。
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
j=0
for i in range(len(nums)):
if nums[i]!=0:
nums[j]=nums[i]
j+=1
for i in range(j,len(nums)):
nums[i]=0
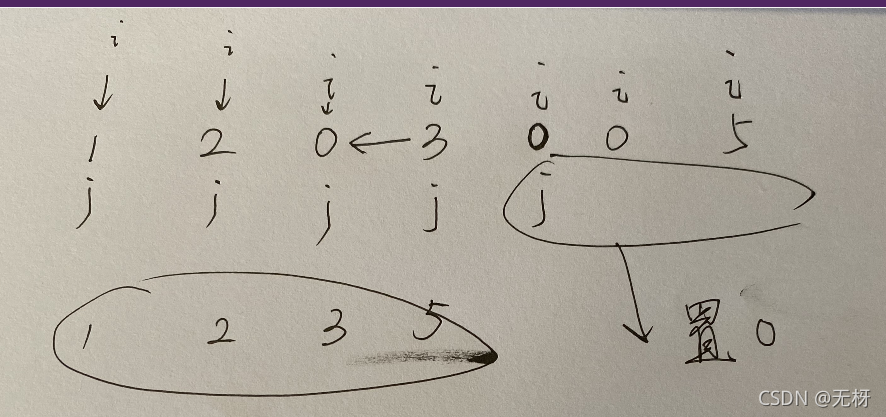
解法二,交换,每次和上述思想差不多,但是不是覆盖,而是交换,因为本身要换的也是0.相当于快速排序的思想,将所有0换到j后面,大于0的部分在前面。但是这里要用单向双指针,不然保持不了相对顺序。
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
for i in range(len(nums)):
if nums[i]:
nums[j],nums[i] = nums[i],nums[j]
j += 1

双向双指针
- 倒序,交换,快速排序(递归)
- 有序数组的两个数之和,正负数有序的平方,也就是满足前后的双数查找
4. 旋转数组
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
解法1,第一种使用求余数的方法,即利用要向右移动k个位置,等于在n-k位置处旋转。
class Solution(object):
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: None Do not return anything, modify nums in-place instead.
"""
n=len(nums)
if k>n:
k=k%n
sel=n-k
res = []
for i in range(sel, sel + n):
res.append(nums[i % n])
for i in range(len(nums)):
nums[i]=res[i]
解法2,分三部分逆序 reverse函数用的就是双指针的做法
class Solution(object):
def reverse(self,nums,i,j):
#return reverse nums
n = len(nums)
l = i
r = j
while l <= r:
nums[l],nums[r]=nums[r],nums[l]
r -= 1
l += 1
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: None Do not return anything, modify nums in-place instead.
"""
#reverse方法
k %= len(nums)
self.reverse(nums, 0, len(nums) - 1)
self.reverse(nums, 0, k - 1)
self.reverse(nums, k, len(nums) - 1)
5. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。 要求时间复杂度On的算法,那肯定不能先算然后排序了 很明显考虑双指针,因为数组非递减,从左右同时到中间的正负分界点,比较左右哪边的平方更大,逆序放入数组
class Solution(object):
def sortedSquares(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
res=[0]*len(nums)
l=0
r=len(nums)-1
pos=len(nums)-1
while l<r:
if nums[l]*nums[l]>nums[r]*nums[r]:
res[pos]=nums[l]*nums[l]
l+=1
else:
res[pos]=nums[r]*nums[r]
r-=1
pos-=1
res[0]=nums[l]*nums[l]
return res
总结
双指针在很多算法中都有用,所以必须掌握,注意最终会和的临界条件即可