前言

一、线性模型






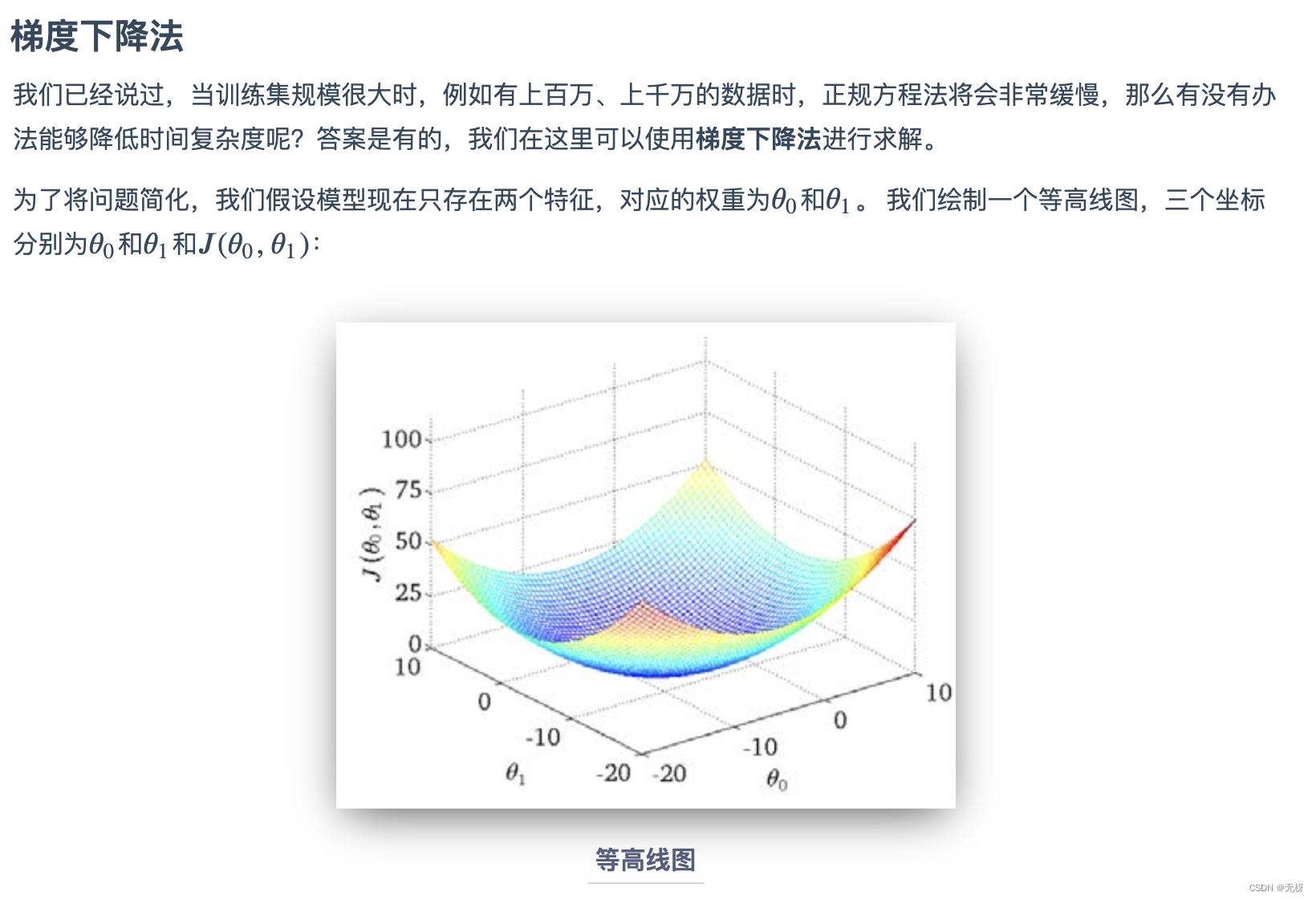



二、线性模型用于词性标注
回到词性标注问题上来 相信通过前面的介绍,你已经对线性模型有了基本的认识,下面我们回到词性标注任务上,简单地介绍一下如何基于多元分类的思想使用线性回归模型进行词性标注。
基本思路 在我们之前的介绍中,你可能会发现,线性模型主要是用于解决机器学习中的回归(regression)问题。也就是说,它预测的最终结果通常是连续值。虽然与对数线性模型相比,线性模型不常用于分类(classification),但在介绍对数线性模型之前,我们仍可以通过一些方法使其运用在分类标注词性上。
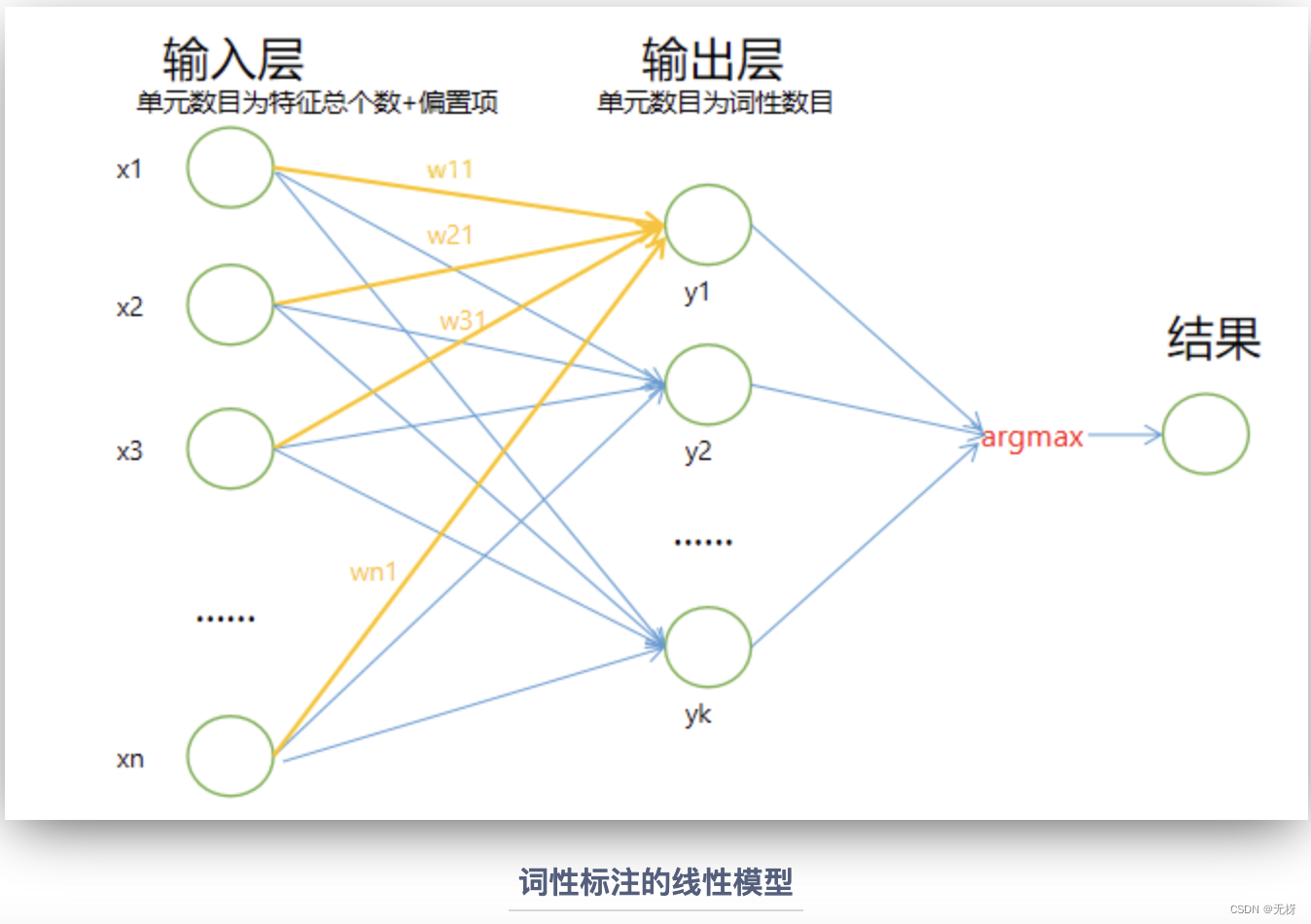
最基本的思想就是,我们通过选取词语的一些特征,训练出一个线性模型,模型的输出为该词语标注为各词性的分值(score),然后我们选取分值最大的词性作为预测的结果。通过这一转化,我们将线性回归模型运用在了分类问题上。
 可以看到,我们一共使用了14种特征模板,其中包含了许多有用的信息,例如词信息,字信息,词缀信息等等。
可以看到,我们一共使用了14种特征模板,其中包含了许多有用的信息,例如词信息,字信息,词缀信息等等。
在实际训练过程中,我们需要先构建特征空间(feature space)。它是训练集中所有特征的集合。构建的方式是:我们每次选取一个词,根据特征模板抽取相应的14种特征,并将其加入到特征空间内。需要注意的是特征空间中不能出现重复的特征。
在这里,我们还可以对特征抽取进行优化。我们观察特征模板可以发现,对于每个样本,每一种特征的模板都需要抽取每一种词性的特征,而对于所有不同的词性,其特征模板的后缀都是相同的。通过计算机中经常使用的段加偏移的思想
 对于模型的训练,我们将采用一种叫做在线学习(Online training)的方式。这是一种经常用于推荐系统的学习算法,方便对模型进行实时训练。你可以把它看作是一种近似于我们之前所提到的随机梯度下降法的学习算法。它每次选取一个实例进行训练。由于样本的标签是经过one-hot处理的离散值,而我们模型的输出是取值范围在负无穷到正无穷 ,所以我们在这里无法使用前述的梯度下降算法进行参数的训练。取而代之的是如下的算法。
对于模型的训练,我们将采用一种叫做在线学习(Online training)的方式。这是一种经常用于推荐系统的学习算法,方便对模型进行实时训练。你可以把它看作是一种近似于我们之前所提到的随机梯度下降法的学习算法。它每次选取一个实例进行训练。由于样本的标签是经过one-hot处理的离散值,而我们模型的输出是取值范围在负无穷到正无穷 ,所以我们在这里无法使用前述的梯度下降算法进行参数的训练。取而代之的是如下的算法。



 上述两种非线性映射函数并不是科学家们一拍脑袋就定义出来的,他们都是有严格的概率统计学证明的。Sigmoid函数是Softmax函数在二分类时的特殊形式,而Softmax函数可以通过信息论中的最大熵模型进行推导。我们根据求解最大熵函数在给定的约束条件下的极值(使用拉格朗日乘子法),可以得到最大熵模型的参数形式,也就是Softmax函数的形式。
上述两种非线性映射函数并不是科学家们一拍脑袋就定义出来的,他们都是有严格的概率统计学证明的。Sigmoid函数是Softmax函数在二分类时的特殊形式,而Softmax函数可以通过信息论中的最大熵模型进行推导。我们根据求解最大熵函数在给定的约束条件下的极值(使用拉格朗日乘子法),可以得到最大熵模型的参数形式,也就是Softmax函数的形式。


总结

前言

一、什么问题用HMM?
使用HMM模型时我们的问题一般有这两个特征:
- 我们的问题是基于序列的,比如时间序列,或者状态序列。NLP中常见的机器翻译、词性标注、分词等任务都可以看作是序列化问题。
- 我们的问题中有两类数据,一类序列数据是可以观测到的,即观测序列;而另一类数据是不能观察到的,即隐藏状态序列,简称状态序列。比如,在机器翻译中,我们可以将源语言文本看作是观测序列,目标语言文本看作是状态序列;又比如,词性标注中,词序列是观测序列,词性序列是状态序列。
二、HMM是什么模型?
生成模型是指对联合概率建模,判别模型是对条件概率建模 ,HMM模型属于生成模型,因为HMM模型中没有建立决策边界,而是直接对联合概率分布建模。当给定观测序列时,我们使用前向算法计算每条状态序列的概率,选取概率最大的状态序列路径作为序列标注的结果
 HMM基于两个重要假设:
HMM基于两个重要假设:
- 齐次马尔可夫假设:马尔可夫性质指的是每个状态值取决于前面有限个状态 例如当前的词性仅依赖于前一个词性是什么。例如,动词后常接名词
- 观测独立性假设:任意时刻的观测状态,仅仅依赖于当前隐藏状态。 即当前词仅与当前词性有关。举例来说,当给定一个词“苹果”,我们根据训练集统计得知名词词性发射至“苹果”的概率远大于其它词性,所以我们可以预测当前词倾向于是名词。
三、HMM用于序列标注训练流程

1. 极大似然估计法(有监督)


2.Baum-Welch算法(无监督学习)
 如果你有机器学习的基础,那你很可能学习过K-Means算法,这是一种无监督的聚类算法。它本质上就是一种EM算法。对于给定的许多个无标签的样本点,K-Means可以将他们聚成任意n个类别。具体的做法是先随机选取数据集中的n个点作为聚类的质心点,计算每个点到每个质心点的距离,将他们归类到距离最小的类别下;然后对于每一个类别,重新计算其质心点;我们反复迭代进行上述的归类和质心计算的步骤,直到质心不再变化。随机初始化和重置质心的过程其实就是EM算法的E步,计算样本点到质心的距离并将其聚类到最近的质心的过程其实就是EM算法的M步。
如果你有机器学习的基础,那你很可能学习过K-Means算法,这是一种无监督的聚类算法。它本质上就是一种EM算法。对于给定的许多个无标签的样本点,K-Means可以将他们聚成任意n个类别。具体的做法是先随机选取数据集中的n个点作为聚类的质心点,计算每个点到每个质心点的距离,将他们归类到距离最小的类别下;然后对于每一个类别,重新计算其质心点;我们反复迭代进行上述的归类和质心计算的步骤,直到质心不再变化。随机初始化和重置质心的过程其实就是EM算法的E步,计算样本点到质心的距离并将其聚类到最近的质心的过程其实就是EM算法的M步。
K-Means算法直接对样本点进行归类,而不是计算每个类别的概率,所以属于Hard EM。Hard EM和 Soft EM的区别和我之前在吴恩达的深度学习课程上看到的 SoftMax和HardMax的区别很像,个人感觉本质是一样。
总结一下,当我们的样本没有给定标注数据,即只有句子没有词性时,我们可以对需要学习的三个参数矩阵进行随机初始化(np.rand),初步确定模型,然后极大化数据的某种似然,调整得到新的参数矩阵,通过不断地迭代,参数矩阵将逐渐收敛,当它们的变化范围缩小到某个可以被接受的阈值时,我们可以停止迭代,将当前的参数矩阵用于预测。
需要注意的是,EM算法无法保证全局最优解,和梯度下降算法非常类似,他们能够稳定达到全局最优的条件都是似然函数(损失函数)是一个凸函数。(PS:似然函数和损失函数的关系我个人认为非常紧密,后面会专门写一篇blog说一下这个问题)
前向后向算法的使用,主要是因为对于网格中的每一个状态,它既计算到达此状态的“前向”概率(给定当前模型的近似估计),又计算到达此状态的“后向”概率(给定当前模型的近似估计)。 这些都可以通过利用递归进行加速计算。使用前向算法和后向算法的相互合作,我们可以得到很多有用的信息,并可以将它们运用在EM算法过程中的极大化似然估计上。(PS:这里的Forward算法和后面Viterbi算法中的Forward算法并不完全相同,这里是 sum-product ,你可以看作是神经网络中的正向传播过程,对于传至当前状态的概率进行求和;而后者是 max-product,对于传至当前状态的概率取最大值 )
这里顺带说一句,前向算法还可以用于计算序列的概率,从而选择模型。如果我们训练了多个词性标注的HMM模型,那么对于一个需要标注的句子,我们可以通过前向算法计算它在不同模型中可能出现的概率,然后选取最大概率的模型用于预测。
3. 隐马尔可夫模型的预测(解码)过程
在这里,我们使用一种叫做维特比(viterbi)算法的动态规划算法进行状态序列的解码,也就是词性序列的预测。
维特比算法是一种动态规划求解篱笆网络(Lattice)的最优路径问题的方法。通俗看懂维特比
 简单阐述一下就是:状态矩阵中,当前节点的值等于上一层各节点的值乘以对应的转移路径的权值所得结果中的最优值(max-product),同时,我们还建立一个回溯矩阵,保存状态矩阵中每个节点的值是由上一层的哪个节点转移而来。当前向传播计算到最后一层时,我们选取最后一层的节点中的最优值,并通过回溯矩阵反向回溯得到对应的最优序列。特别地,在隐马尔可夫模型中,我们在前向传播计算每个节点最优值的时候,还需要考虑发射概率。
简单阐述一下就是:状态矩阵中,当前节点的值等于上一层各节点的值乘以对应的转移路径的权值所得结果中的最优值(max-product),同时,我们还建立一个回溯矩阵,保存状态矩阵中每个节点的值是由上一层的哪个节点转移而来。当前向传播计算到最后一层时,我们选取最后一层的节点中的最优值,并通过回溯矩阵反向回溯得到对应的最优序列。特别地,在隐马尔可夫模型中,我们在前向传播计算每个节点最优值的时候,还需要考虑发射概率。
通过维特比算法,我们可以较快的利用训练好的模型去预测一个句子的最大概率词性序列,并输出。 在实际运用模型的过程中,我们还会发现这样的一个问题:训练得到的参数矩阵很可能是较为稀疏的,例如从一个词性从未发射到某个单词过。同时,训练集的规模有限,不可能包含所有的词和词性。由于状态矩阵的转移涉及概率的累乘,上述未登录的情况将导致发射或转移或初始概率为0,进而使得前向传播计算出的整条序列地概率为0 为了解决零概率问题,我们需要还引入平滑方法,例如Laplace平滑等 平滑参考
总结
至此可以了解HMM的详细训练和解码流程