一、PQ是什么？
Faiss是什么
Faiss是FAIR出品的一个用于向量k-NN搜索的计算库，其作用主要在保证高准确度的前提下大幅提升搜索速度，根据我们的实际测试，基于1600w 512维向量建库，然后在R100@1000 （即召回top 1000个，然后统计包含有多少个实际距离最近的top 100）= 87%的前提下单机15线程可以达到1000的qps，这个性能应该是可以满足大部分的推荐系统召回模块性能需求了。
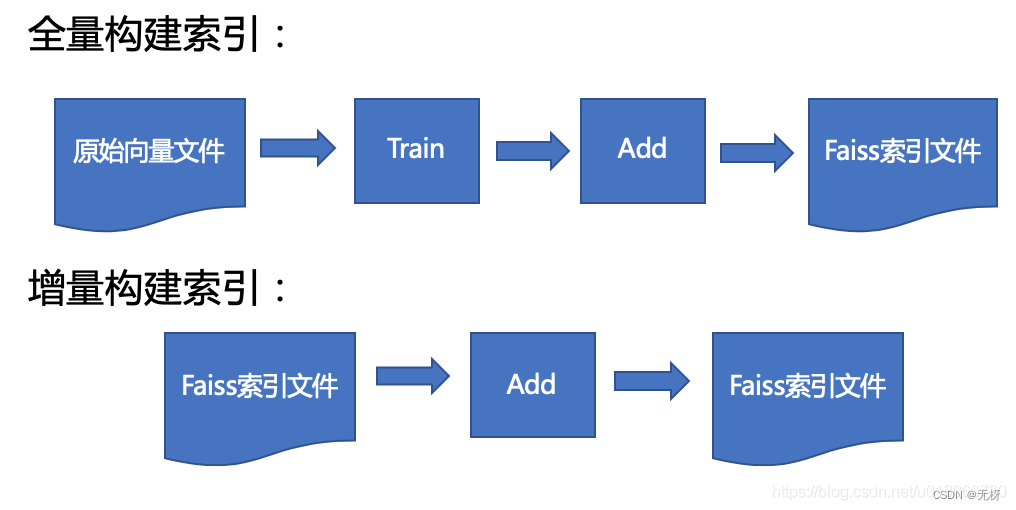我们可以大概的看一下，首先FAISS对原始的doc向量库做一个预训练，然后构建原始faiss索引文件
增量索引也很方便，增删改查都很方便，只有增量的量级和原始doc的差不多的时候，可能需要重新构建全局doc索引
Produce Quantizer（乘积量化）
首先我们看一下乘积量化的基本思想：
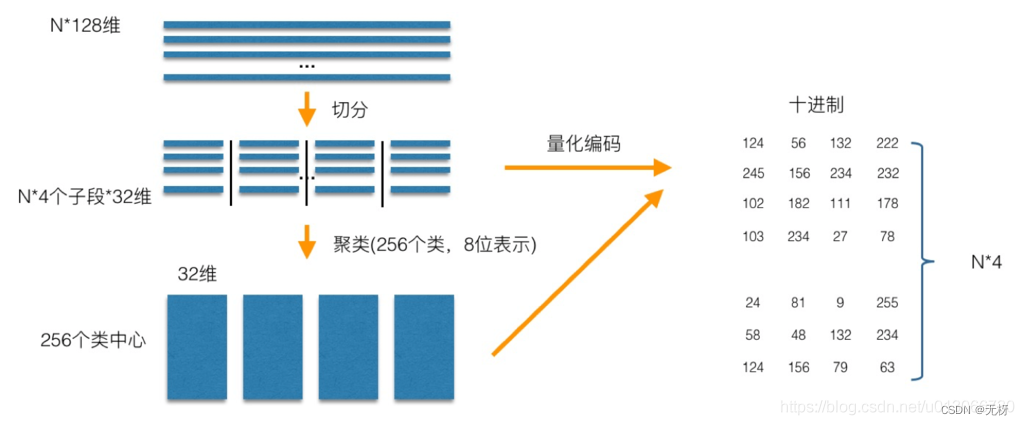
PQ有一个Pre-train的过程，一般分为两步操作，第一步是Clustering，第二部是Assign，这两步合起来就是对应到前文提到Faiss数据流的Train阶段
Clustering：
可以以N个128维的向量库为例，首先这里有一个超参M，将这些128的向量切分为N个M（128/M），这里我们看到是M=4，因此有N个432的向量段 对于每个子空间，通过类似kmeans这样的聚类算法将每一段的向量聚成K个类，建立码本，从而训练样本中每个子向量都可以用聚类中心来近似。 以上述为例，所以向量库的每一个向量就被切分成了4段，然后把所有向量的第一段取出来做Clustering得到256个簇心（256是超参K），再把所有向量的第二段取出来做Clustering得到256个簇心，直至对所有向量的第N段做完Clustering，从而最终得到了256*M个簇心，
Assign
做完Clustering就开始对所有向量做Assign操作。这里的Assign就是把原来的N维的向量映射到M个数字，以N=128，M=4为例，首先把向量切成四段，然后对于每一段向量，都可以找到对应的最近的簇心 ID，4段向量就对应了4个簇心 ID，一个128维的向量就变成了一个由4个ID组成的向量，这样就可以完成了Assign操作的过程。
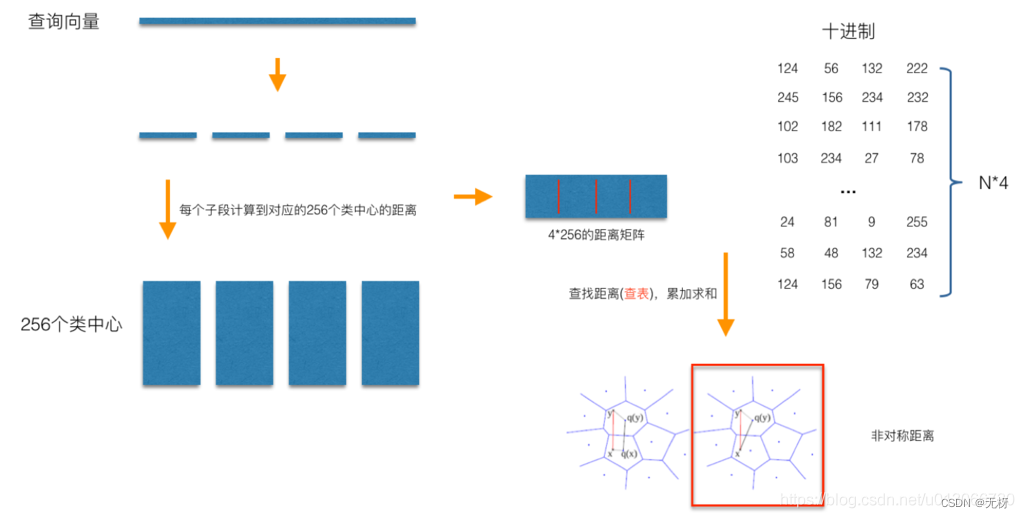
PQ-search：
同样是以N=128，M=4为例，对于每一个查询向量，以相同的方法把128维分成4段32维向量，然后计算每一段向量与之前预训练好的簇心的距离，得到一个4*256的表，就可以开始计算查询向量与库里面的向量的距离，而PQ优化的点就在这里，在计算查询向量和向量库向量的距离的时候，向量库的向量已经被量化成M个簇心 ID，而查询向量的M段子向量与各自的256个簇心距离已经预计算好了，所以在计算两个向量的时候只用查M次表，
比如的库里的某个向量被量化成了[124, 56, 132, 222], 那么首先查表得到查询向量第一段子向量与其ID为124的簇心的距离，然后再查表得到查询向量第二段子向量与其ID为56的簇心的距离。最后就可以得到四个距离d1、d2、d3、d4，查询向量跟库里向量的距离d = d1+d2+d3+d4。
所以在提出的例子里面，使用PQ只用4×256次128维向量距离计算加上4xN次查表，而最原始的暴力计算则有N次128维向量距离计算，很显然随着向量个数N的增加，后者相较于前者会越来越耗时。
因为PQ采用的其实是近似距离，处于同一个簇心的向量段离query的距离是一样的。但是因为分成了M段，因此误差会近似减少，因此PQ加快速度但是会损失一定的精度。
二、IVF-PQ是什么？
Inverted File System倒排索引 IVF-PQ：倒排索引量化 IVF本身的原理比较简单粗糙，其目的是想减少需要计算距离的目标向量的个数，做法就是直接对库里所有向量做KMeans Clustering，假设簇心个数为1024，那么每来一个查询向量，首先计算其与1024个粗聚类簇心的距离，然后选择距离最近的top N个簇，只计算查询向量与这几个簇底下的向量的距离，计算距离的方法就是前面说的PQ，Faiss具体实现有一个小细节就是在计算查询向量和一个簇底下的向量的距离的时候，所有向量都会被转化成与簇心的残差，这应该就是类似于归一化的操作，使得后面用PQ计算距离更准确一点。使用了IVF过后，需要计算距离的向量个数就少了几个数量级，最终向量检索就变成一个很快的操作。
其实就是一个分桶的操作
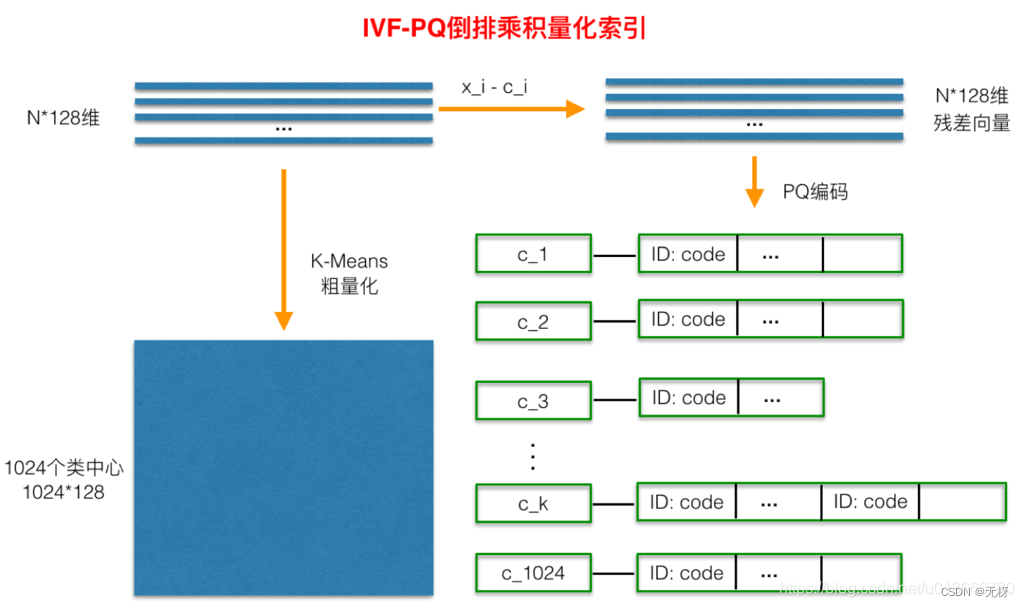IVF-PQ适用于更大数据量的检索操作
但同时损失的精度也更多
可以用二级搜索的方式。通过乘积量化得到TopK的近似结果，同时对query和TopK 对应的原始向量进行暴力检索，这个可以提高准确率。
总结
以上就是PQ的基本思路，和基于空间划分的KD-tree以及基于图构建索引的HNSW和NSG的思路还是不一样的。
