题目
136.给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
集合解法
-
使用集合存储数字。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字。
-
使用集合存储数组中出现的所有数字,并计算数组中的元素之和。由于集合保证元素无重复,因此计算集合中的所有元素之和的两倍,即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次,其余元素都出现两次,因此用集合中的元素之和的两倍减去数组中的元素之和,剩下的数就是数组中只出现一次的数字。
哈希表解法
建立hash表然后计算一下我们可以使用哈希映射统计数组中每个元素的出现次数。对于哈希映射中的每个键值对,键表示一个元素,值表示其出现的次数。
在统计完成后,我们遍历哈希映射即可找出只出现一次的元素。
class Solution:
def singleNumber(self, nums: List[int]) -> int:
freq=collections.Counter(nums)
for num,occ in freq.items():
if occ==1:
return num
- 时间:数组为n要遍历一遍才能得到每一个数字的出现次数,因此时间复杂度为O(n)
- 空间:因为要存储不重复的数字,因此为[n/2]+1,因此空间复杂度也是O(n)
位运算解法
位运算解法1:
对于这道题,可使用异或运算⊕。异或运算有以下三个性质。
- 任何数和 00 做异或运算,结果仍然是原来的数,即 a ⊕ 0=a 。
- 任何数和其自身做异或运算,结果是 0,即 a ⊕ a=0。
- 异或运算满足交换律和结合律,即 a⊕b⊕a=b⊕a⊕ a=b⊕(a⊕a)=b⊕0=b。
数组中的全部元素的异或运算结果总是可以写成如下形式: 0⊕0⊕⋯⊕0⊕am+1=am+1 am+1即那个出现一次的数字。因为其余出现两次的数字都异或成0了。
复习一下python的位运算:
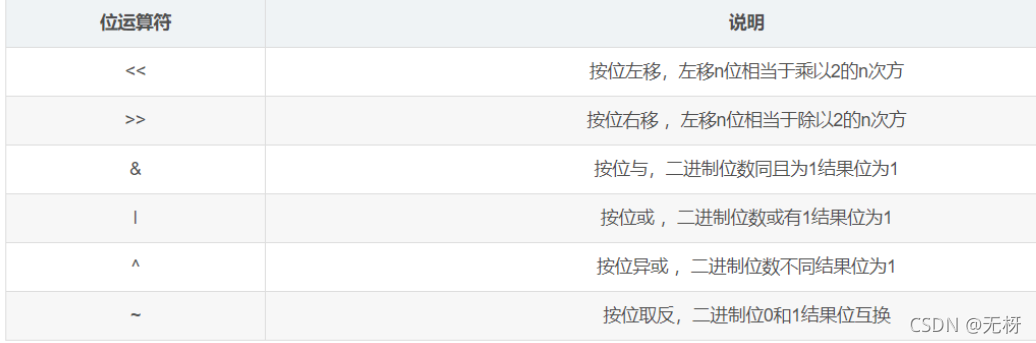
python:
class Solution:
def singleNumber(self, nums: List[int]) -> int:
ans=0
for num in nums:
ans^=num
return ans
- 时间复杂度:O(n),其中 n 是数组长度。只需要对数组遍历一次。
- 空间复杂度:O(1)。
- 运行速度超越99%
位运算解法2
但是上述位解法并不适用于其余数字出现为奇数次的时候,如果对137题解答:
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次请你找出并返回那个只出现了一次的元素。
那么上述解法则不适用了。
因此我们可以通过对每一位上的二进制位加法,来实现找到答案位。
因为int(32位整数),对每一个数的二进制位计算0或者1,非答案二进制位的1或者0的和都是3的倍数,而答案位却是3的有余数有1。
因此我们可以通过在32位上对每一个数字的二进制位做加法,所得如果不能整除3,那就是答案所在的二进制位。
class Solution:
def singleNumber(self,nums:List[int])->int:
ans=0
for i in range(32):
total=sum((num>>i)&1 for num in nums)
if total%3==1:
if i==31:
ans-=(1<<i)
else:
ans|=(1<<i)
return ans
- 时间复杂度:O(nlogc),其中n 是数组长度。log(c)是二进制位数,本题是log(2^{32})=32。
- 空间复杂度:O(1)。因为借助了常数级的空间,总共32位